ANAL PRECISION

Numbers are in degrees for angles, mm for linear

EQUATIONS:

1) p = sqrt(sqrt((f*f) + 0.0625*(d*d))/(1/(J*w)))

3) f = 0.5*d/tan(A/2)

4) f = sqrt(((p^2)*(1/(J*w))^2)/(0.25*d)^2)

Example:

A 4x5 pinhole camera, 50mm lens with a red filter to bring out the clouds.

Diagonal of 4x5 is 152mm

Focal length is 50mm

Red light is 0.00065mm [blue is 0.00045 and green is 0.00055]

What is the size of the pinhole?

p = sqrt(sqrt((50x50) + 0.0625x(152x152))/(1/(3.74x0.00065)))

p = sqrt(sqrt(2500 + 1444)/411)

p = sqrt(62.8/411)

p = 0.391mm

Here is a table of values for green light and common film formats.

ANGLE OF VIEW

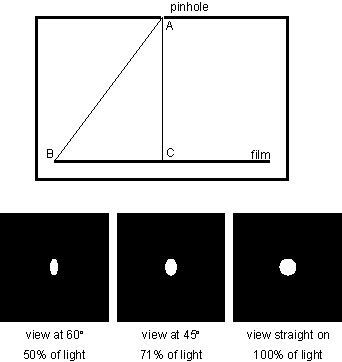
The above equations do not give the same values as the previous web page as they account for the angle of view as well. The difference will be more pronouced at wider angles of view because of the difference between the pinhole to film plane distance at the center of the field and at the extremes.

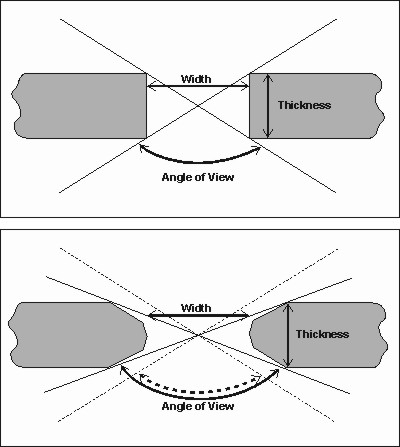
In the above figure, note that the distance from A to B is longer then from A to C. To account for this the formulas take the average value. BUT, the size of the pinhole is also changing. In the bottom half of the above figure, we see how the shape of the pinhole changes with angle of view. This is assuming an infinitely thin pinhole, which is never the case, so . . .

What about the thickness of the the pinhole?

With some complicated math and knowing the width and thickness of a pinhole a graph showing the angle of view whereby we lose 1, 2, 3 stops of light can be made. If you are really conservative, use the one stop line, otherwise the two stop line is probably still acceptable and use the three stop if you are really trying to stretch it and are using a film with lots of latitude.

Width of the brass shim stock is in thousandths of an inch, but the equations are metric, so a need to convert is necessary.

1mm = 39.4 thousandths of an inch or 1 thousandths of an inch = 0.0254 mm

So, if you have a 0.300 mm pinhole on 0.001" shim stock [1 thousandths of an inch]

0.3 x 39.4 = 11.82 thousandths of an inch and the ratio becomes 11.82/1 or 11.82

if the shim stock was 2 thousandths then it would be 11.82/2 or 5.91

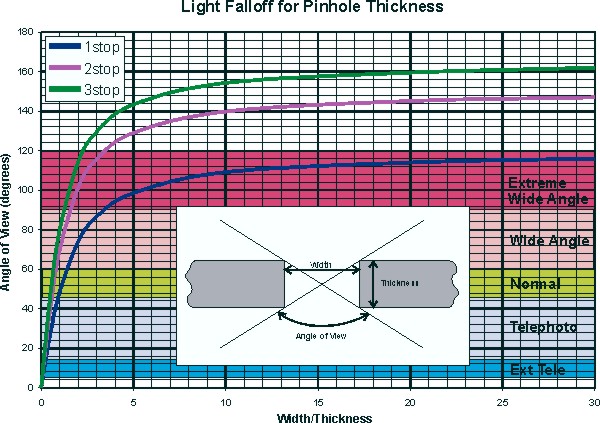
You are not likely to have much trouble with this until you get to very small pinholes. The "worst" of the precision pinholes from Electron Microscopy Sciences, using the copper grids [see], is the 0.075mm pinhole, that has a 0.018mm thickness, or 4.2 W/T on the above graph. The reading for one stop is about 96 degrees, a wide angle lens. Still pretty good.

Where you are likely to get into trouble is with the precision platinum pinholes in the extremely small range. At 0.010mm width and 0.100 thickness, your angle of view is VERY limited. These sizes are of limited use to the hobbiest anyway.

This assumes of course, that you have a straight hole. If you round the edges, somehow, then you can extend the angle of view somewhat. See medium tech. Hmm, might be an advantage to doing your own.